Stellenwertnotation
[ zurück ]
[ Stichworte ]
[ Die Hyper-Bibliothek ]
[ Systemtheorie ]
[ Meine Bücher ]
![bild]()
|
Darüber, was eine Zahl ist, herrscht Chaos.
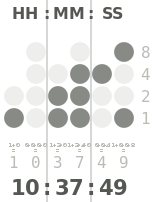
Die Anwendung der Stellenwertnotation versteht jeder Kindskopf, aber wie sie erläutert werden könnte, ist den meisten Menschen ein Rätsel. Es ist vergleichbar mit der analogen Uhr, auf welcher jeder die Zeit ablesen kann, ohne zu sehen, was er dabei tut.
|
![bild]()
|
Zahl
Zahlzeichen
|
|
Als Stellenwertnotation bezeichne ich ein Notation, bei welcher der Wert jeder Ziffer von deren Position abhängt.
Die Stellenwertnotation stammt wohl aus Indien, hier wurde sie durch die Bücher von L. Fibonacci und Adam Ries bekannt und üblich.
Die Stellenwertnotation führte auch die Null für nicht durch andere Ziffern besetze Stellen ein.
![bild]()
|
1
2
3
4
5
6
7
8
9
|
10
11
12
13
14
15
16
17
18
19
|
|
![bild]()
|
Bildquelle: Wikipedia
|
Eine verbreitete Alternative ist das Additionssystem, bei welchem der Wert jeder Ziffer .....
===========
Ein Stellenwertsystem, Positionssystem oder polyadisches Zahlensystem ist ein Zahlensystem, bei dem die (additive) Wertigkeit eines Symbols von seiner Position, der Stelle, abhängt. Beispielsweise besitzen im weitverbreiteten Zehnersystem für den Beispiels-Wert „127“ die Ziffer „1“ den Wert 1 · 100, dazu addiert sich für die Ziffer „2“ der Wert 2 · 10 sowie für die „7“ 7 · 1 – die Symbole „1“, „2“ und „7“ besitzen eine Wertigkeit, die davon abhängt, an welcher Position/Stelle sie in der Zahl stehen. Unter der Annahme eines endlichen Vorrats an Symbolen (meist Ziffern oder Zahlzeichen genannt, im Beispiel „0“…„9“) hängt die Anzahl der erforderlichen Stellen logarithmisch von der Größe der dargestellten Zahl ab – im Unterschied zu Additionssystemen, bei denen dieser Zusammenhang (asymptotisch, d. h. für ganz große Zahlen) linear ist.
Die Größe {\displaystyle b}b des Ziffernvorrats spielt eine entscheidende Rolle. Im Zehnersystem-Beispiel ist der Ziffernvorrat „0“ bis „9“, das sind {\displaystyle b=10}b=10 verschiedene Symbole. Bei den wichtigen ganzzahligen Systemen ist der Wert der dargestellten Zahl gleich die Summe der Produkte des jeweiligen Ziffernwerts mit seinem Stellenwert, also ein Polynom in {\displaystyle b}b mit den Werten der Ziffern als Koeffizienten; im Beispiel 127:
Zahlenwert = „1“ · 102 + „2“ · 101 + „7“ · 100.
Deshalb wird {\displaystyle b}b als Basis oder Grundzahl des Systems bezeichnet. Die Darstellung von Zahlen bezüglich einer Basis {\displaystyle b}b wird oft auch ihre {\displaystyle b}b-adische Darstellung (nicht zu verwechseln mit {\displaystyle p}p-adischen Zahlen) genannt. Jede ganze Zahl {\displaystyle b\geq 2}b\geq 2 eignet sich als Basis für ein Stellenwertsystem.[1]
Beispiele für Stellenwertsysteme sind das im Alltag gewöhnlich gebrauchte Dezimalsystem (dekadisches System mit der Basis 10), das in der Datenverarbeitung häufig verwendete Dualsystem (dyadisches System mit der Basis 2), das Oktalsystem (mit der Basis 8), das Hexadezimalsystem (mit der Basis 16) sowie das Sexagesimalsystem (mit der Basis 60). Ein Beispiel für ein Zahlensystem, das kein Stellenwertsystem ist, ist das der römischen Ziffern. Es handelt sich dabei um ein Additionssystem.
[wp]
