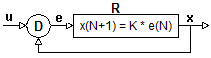kybernetische Simulation
[ zurück ]
[ Stichworte ]
[ Literatur ]
[ Die Hyper-Bibliothek ]
[ Systemtheorie ]
[ Meine Bücher ]
Als kybernetische Simulation bezeichne ich ein Verfahren, mit welchem ich untersuche, wie sich bestimmte Variablen eines Systems im Laufe der Zeit in Abhängigkeit der jeweilig vorausgesetzten Bedingungen verhalten. Das Verfahrens wird auch als System Dynamics bezeichnet, wobei die System Dynamics dadurch berühmt wurde und in Verruf kam, dass der Club of Rome deren Resultate in Prognosen über die Welt überstrapazierte.
Als Simulation bezeichne ich das Verfahren, weil ich es auf ein Modell anwende und als kybernetisch bezeichne ich es, weil das Modell aus Regelkreisen besteht, die Bedingungsvariablen mit Verhaltensvariablen durch berechenbare Funktionen verknüpfen, was formal ich durch x=f(y) ausdrücke.
Dabei ist gleichgültig, ob die Simulation auf ein Ereignis bezogen wird, das ich technisch reproduzieren will oder nicht. N. Wiener sprach deshalb von Kontrolle im Tier und in der Maschine. (M)Ein Standardbeispiel ist die thermostatengeregelte Heizung, also eine Maschine bei welcher ich die Variablen Aussentemperatur und Innentemperatur in eine funktionale Beziehung setze. Die Simulation kann dazu dienen, zu kontrollieren, ob die von mir hypothetisch vermuteten, gesetzmässigen Zusammenhäge sich quantitativ verifizieren lassen, oder dazu, wie ich eine Heizung optimal herstelle und einrichte. Es geht in beiden Fällen darum, den Verlauf von Variablenwerten als Funktion von anderen Variablen innerhalb eines geschlossenen Systems zu beschreiben.
|
Der kybernetische Regelkreis hat drei Elemente: den Differenzbildner (D), den Regler (R) und die Strecke (S). Der Differenzbildner (D) verrechnet den Istwert "x" und den Sollwert "u" und erzeugt daraus die Differenz "e", die als Wert in den Regler (R) eingeht, dessen Reaktion als Stellgrösse "y" den Zustand der Strecke steuert, der dann als "x" wieder zum Differenzbildner zurückgeführt wird, was ich als Feedback bezeichne. Man kann sagen, dass der Regler eine Massnahme auslöst, die dann in der Strecke ihre Wirkung zeigt. Bei einer Heizung besteht sie Massnahme beispielsweise in stärkerem Heizen, was sich in den Radiatoren dann als höhere Temperatur auswirkt. Bis die Raditoren reagieren vergeht einerseits eine gewisse Zeit, die ich als Totzeit bezeichne, und andrerseits werden die Radiatatoren auch durch die Raumtemperatur abgekühlt, was in Bezug auf die Regelung als Störung erscheint.
Im Blockdiagramm-Schema des Modelles repräsentieren die Pfeile Signale mit einem variablen Wert und die Funktionsblöcke programmierte Prozessoren, die dem Input einen Output zuordnen. Ich stelle hier nur ein Verfahren dar, das ich als exemplarisch für das prinizipielle Verständnis betrachte. Ich erläutere eine zeitdiskrete Regelung mit einer Totzeit.
|

|
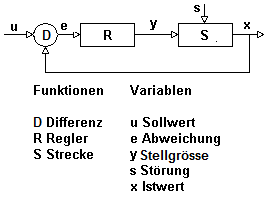
 Regelkreis-Schema Regelkreis-Schema
|
Zeitdiskret bedeutet, dass Regelung einem Takt unterliegt, wodurch die Signale immer einem bestimmten Zeitpunkt zugeordent sind. In der Notation x(N+1) = Kp * e(N) bedeutet, dass "x" einen Takt später gemessen wird als "e". In sehr vielen Fällen fallen die Daten ohnehin zeitdiskret an. In der Modellierung werden die Variablen als numerische Werte in Zeitreihen berechnet und mithin als "x" t ... t(n) dargestellt. Das gewählte Taktintervall wird wird nach inhaltlichen Erwägungen gewählt, im einfachsten Fall wählt man die Totzeit "τ" (tau).
Ich will gebe dazu anschauliche Beispiele. Wenn ich mein Auto bremse wird der Druck auf das Bremspedal nicht wie früher kontinuierlich an die Bremse weitergegeben, sondern es wird damit ein Servomotor gesteuert, der durch ein Antiblockiersystem getaktet wird. Ich habe dabei das Gefühl, dass ich kontinuierlich bremse, aber der Bremsmechanismus operiert im Takt des ABS. Auch die von einer Heizung erzeugte Raumtemperatur mag man als einen sich kontinuierlich verändernden Wert betrachten. Das digitale Thermometer zeigt zu einem gebenen Zeitpunkt aber beispielsweise 15 oder 15,27 Grad, also einen diskreten Wert an. Wenn der Sollwert auf 20 Grad eingestellt ist, ergibt sich eine Abweichung von 5 oder von 4,73 Grad, also ein diskreter Wert, der im Regler verrechnet wird. Ein grosser Vorteil der zeitdiskreten Modellierung besteht darin, das ich dazu keine höheren mathematische Kenntnisse brauche, während ich kontinuierliche Prozesse nur mit Differentialgleichungen beschreiben kann.
Indem ich den Takt einführe, unterscheide ich die Kybernetik auch explizit von der Mathematik, die keine Zeit, dafür aber Paradoxien kennt. Kybernetik ist wie Informatik eine Engineeringdisziplin und in diesem Sinn eine materielle Wissenschaft, die hergestellte Gegenstände oder Gegenstände als hergestellte beschreibt. Beim Simulieren rechne ich zwar mit Zahlen, aber die Zahlen beziehen sich auf Referenzobjekte in der wirklichen Welt, während Mathematik nur eine Geisteswissenschaft ist, in welcher die wirklichen Welt noch die Zeit eine Rolle spielt.
Ich beschreibe im Folgenden die einzelnen Funktionen, die in den Funktionselementen des Regelkreises realisiert sind.
Die einfachste Funktion hat der Differenzbildner "D". In ihm wird - im Takt - die Differenz "e" zwischen dem jeweils aktuelle Sollwert "u" und dem jeweils aktuellen Feddback- oder Istwert "x" berechnet. Die Differenz ist der Input des Reglers "R".
Natürlich muss dazu "x" in einer geeigneten Art vorliegen, was in manchen Fällen durch die Modulation in einem Messblock (Sensorgerät) gewährleistet wird, der beispielsweise ein analoges in ein digitales Signal umwandelt. Die Dampfmaschinenregelung von J. Watt beispielsweise hat als Ausgang eine Drehzahl der Welle, die natürlich kein Zahl sondern eine Bewegung ist, der ich eine Zahl zurodne.
Der Regler (R) erzeugt aufgrund des Inputs "e" eine Massnahme, die die Stellgrösse "y" ausgibt. Der Regler repräsentiert die Funktion y=f(e). Ich unterscheide drei verschiedene Entwicklungsstufen des Reglers:
Der einfachste Regler heisst Proportional-Regler (P). Seine Funktion ist y(N+1) = K * e(N). Das bedeutet, dass der Wert von "e" mit einer (Proprotionalitäts)-Konstante (K) verrechnet wird. Dabei ist das Verhalten von der Wahl von u und K und den Anfangsbedingungen abhängig.
|

|
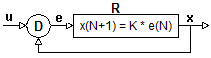
|
Natürlich kann "u" auch sehr verschieden gewählt werden. Was im Alltag getan wird, ist beispielsweise die Unterscheidung zwischen Tag- und Nachttemperatur. In einem komplizierteren Regelkreis kann "u" auch von anderen Grössen wie "x" anhängig gemacht werden. In diesem einfachsten Fall zeigt sich, dass beispielsweise eine Sägezahnfunktion von "u" ein Aufschwingen von "x" ergibt, wenn K = 1 gewählt wird.
Wenn K optimaler gewählt wird, beispielsweise K=0,5 kann "x" rasch stabil einschwingen, beispielsweise bei "u" konstant =1, wird "x" nach wenigen Schritten auf 0,67 konstant bleiben - wie man ohne weiteres "von Hand" nachrechnen kann.
Die Wahl der Bedingungen führt also bereits bei dieser einfachen Reglerfunktion zu stabilem oder instabilem Verhalten.
- Bevor aufwendigere Regler behandelt werden, soll noch eine weitere Unterscheidung eingeführt werden: aktive versus passive Gesetze. Passiv sind Funktionen die nur reagieren, aktiv sind solche, die Fälle unterscheiden, was als Ent-scheidung gesehen werden kann. Es geht darum, wie vergangene Verhaltensweisen und projiziert künftige Verhaltensweise berücksichtigt werden und darum, dass verschiedene Verhalten zur Disposition stehen. Vom Einkommen kann ich passiv abhängig machen, wieviel Geld ich ausgebe. Aktiv kann ich davon abhängig machen, welche Feriendestinationen ich in Betracht ziehe. Ich kann ausserdem künftige Ereignisse wie Lohnerhöhungen in Betracht ziehen.
Auch wenn mein Bankkontostand kleiner wird, muss ich nicht sofort reagieren. Ich kann die Reaktion verzögern.
|

|
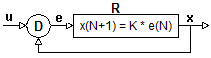
|
[3digi]
[]
Ein passives Glied ist beispielsweise:
K * y(N) = x(N) + T1 * Δx(N) + T2 * Δ2 x(N)
wobei T und K Konstanten sind und
und die Teile von x als Widerstand, Trägheit gedeutet werden ....
PID-Regler : y(N) = Kp * e(N) + Ki * Summe (E(N) + Kd * Δ e(N)
heizung_funktion.png
heizung.png
[wp]