|
|
|
Beschreibungen .... Anweisung... (Anmerkung 2).
|
Das nebenstehende Schema zeigt |
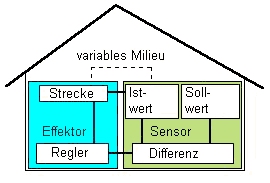
|
|
|
|
Beispiele:
|
| Zum Teil 2 | |
| Zum Teil 3 - inkl. speziellem Abschnitt über Digitalregler | |
| Zum Teil 4 inkl. RT-FAQs und Literatur | |
| PDF-File des ganzen Kurses (Bildteil getrennt im Anschluss, insgesamt ca. 1,45 MB) |
Hinweis des Autors: Im folgenden soll der Versuch gemacht werden, die Begriffe Steuerung und Regelung verständlich zu machen und eine kleine Einführung in die Regelungstechnik zu geben. Die Ausführungen können im Einzelnen vielleicht nicht immer streng konform mit den Definitionen und Vorschriften der DIN oder anderer Regelwerke sein, die 'Profis' mögen das verzeihen, - es soll, wie gesagt, mehr auf Verständlichkeit Wert gelegt werden.
Die Steuerung ist ein Vorgang, bei dem einem zu steuernden 'Objekt' (Prozeß) feste Stellwerte vorgegeben werden. Inwieweit die Steuerung sich dann auch 'darum kümmert', ob das Objekt mit den vorgegebenen Stellwerten den gewünschten Effekt 'erbringt', das ist eine Frage ihrer Aufwendigkeit (sozusagen ihrer 'Intelligenz'), - im primitivsten Fall 'tut' sie es überhaupt nicht! Man kann zwischen 'konditionellen Steuerungen' und 'zeitlichen Ablaufsteuerungen' (Beispiel: programmierte Temperaturabläufe bei Heizvorrichtungen) unterscheiden, - in der Praxis sind Steuerungen jedoch meist eine mehr oder weniger komplexe Mischung aus beidem, wie zum Beispiel bei Waschmaschinen- oder Ampelsteuerungen. Vordergründig erscheint die Steuerung weniger kompliziert zu sein als eine Regelung, weil einen bei der Regelung zunächst die etwas umfangreicheren mathematischen Formeln für die Regelalgorithmen und die komplizierten Prozeduren der Systementwicklung etwas 'erschlagen'. Im Grunde genommen ist aber die Steuerung eines Prozesses meistens der 'overhead' mehrerer Regelvorgänge und beinhaltet bei weitem mehr 'Intelligenz' als eine Regelung. Sieht man von der Stellwertausgabe bei der Regelung, die ja formal auch als Steuerung bezeichnet werden könnte, einmal ab, so kann man feststellen, daß Regelungen sehr häufig die 'slaves' von Steuerungen sind. Steuerungen beinhalten ein relativ kompliziertes 'Konditions- und Ablaufprogramm'. Derartige Programme enthalten heute häufig schon hochentwickelte KI-Moduln, wie z.B. Expertensysteme mit ANNs (künstliche Neuronale Netzwerke) und Fuzzy Logik.
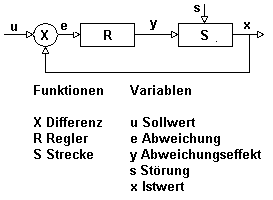
Eine Regelung kümmert sich dagegen ziemlich zwingend um die Einhaltung gewünschter Bedingungen 'in einem Objekt'. Das Objekt nennt man in diesem Metier '(Regel-)Strecke'. Der 'Operator', der die 'Einhaltung' bewerkstelligt, ist der 'Regler'. Der Regler wirkt verändernd auf die Strecke mit Hilfe eines 'Stellsignals', oft auch 'Stellwert' genannt, welches(n) er ausgibt (elektrisches, pneumatisches o.a. Signal). Diese Veränderung wird bewirkt durch eine spezielle Vorrichtung 'vor oder innerhalb' der Regelstrecke, - das 'Stellglied' (auch 'Aktor') (Beispiele: Nadelventile, Drosselklappen, Hubmagnete, Triacs, Thyristoren, Leistungstransistoren u.v.a.). Meßglieder (Sensoren, Analysatoren), die sich an den verschiedensten Meßorten 'vor, auf oder hinter' der Strecke befinden, versorgen den Regler mit einer 'Istwertinformation'. Eingeweihte haben es schon bemerkt, daß bis hierher der Begriff 'Regelkreis' hartnäckig vermieden wurde. Bei der Kategorisierung von Reglern ist nämlich eine der wichtigsten Einteilungen die Frage, woher bezieht der Regler den Istwert und in welcher Weise verarbeitet er ihn. Wenn der Regler den Istwert - sozusagen als Ergebnis seines Wirkens - vom 'Ende' der Strecke erhält, dann spricht man von einem 'feedback' oder zu deutsch einer 'Signalrückkopplung'. In solchen Fällen läuft die Regelung in einem rückgekoppelten Kreislauf ab, - dem 'Regelkreis'. Dies stellt die klassische Form der Regelung dar. Ein Regelkreis (siehe Abb.1, rechts hinscrollen!) besteht aus: Regler, Meßglied (--> Istwert, Meßwertrückkopplung), Stellglied(-->Stellwert, Stellsignalvorgabe) und die 'Bedingung', die der Regler aufrechterhalten soll, also der 'gewünschte Istwert' muß dem Regler in Form des sogenannten 'Sollwerts' mitgeteilt werden. In einem Regelkreis erhält der Regler vom Meßglied den Istwert gemeldet, vergleicht diesen mit dem Sollwert und ermittelt mit Hilfe einer 'Vorschrift' (Algorithmus, z.B. PID-Algorithmus - es gibt aber auch andere!) einen Stellwert und gibt diesen an das Stellglied aus. Derartige Regler können im einfachsten Fall analogelektronische Schaltungen sein. Der Regler wird nun aufgrund von Algorithmus und Rückkopplung 'gezwungenermaßen' ständig die Istwertrückmeldung beobachten und den Stellwert solange verändern, bis er die 'Sollwertabweichung' (Differenz zwischen Ist- und Sollwert) 'nach seinen Möglichkeiten (Parametrisierung, Qualität des Algorithmus) minimiert hat', er kommt dabei nur scheinbar zur Ruhe (rückgekoppelte Systeme sind schwingfähig, Frage des 'Dämfungskriteriums'). Wenn der Sollwert für einen Regelkreis über längere Zeit fest vorgegeben wird, besteht die Aufgabe des Reglers 'lediglich' darin, auftretende 'Störungen' der Strecke zu beseitigen. Die Fachsprache nennt das 'Regeln auf Störung' Wird dagegen von einem übergeordneten Steuerungsablauf eine zeitliche Veränderung des Sollwerts vorgegeben, dann arbeitet der Regler im Regelkreis 'auf Führung'. Beim Arbeiten auf Führung muß der Regler 'trotzdem' auch imstande sein, kurzfristige Störungen zu beseitigen, man könnte daher diese Aufgabe als 'anspruchsvoller' bezeichnen. Wie aus der schematischen Darstellung (Abb.1) zu erkennen ist, kann ein 'klassischer Feedbackregler' eigentlich nur eine einzige Größe 'beregeln'. Man spricht deshalb von einer 'Eingrößen-Regelung'. Tritt bei einer Regelung die Notwendigkeit auf, aus mehreren Meßgrößen eine oder gar mehrere Stellgrößen in ein und demselben Regelkreis 'hervorzubringen', dann liegt der komlpizierte Fall einer 'Mehrgrößen-Regelung' vor, der in der klassischen Regelungstechnik nur mit komplexen 'Reglerschaltungen', wie z.B. Kaskadierungen, Master-Slave-Schaltungen u.a. verwirklicht werden kann. Systemanalyse und Systementwurf werden sehr schwierig. Ein einfaches Beispiel für eine Mehrgrößenregelung wäre ein KFZ-Abstandsregelungssystem, bei dem aus Eigengeschwindigkeit, Geschwindigkeit des Vorherfahrers und Fahrzeugabstand das Abbremsen und die Gasbetätigung eines Fahrzeugs geregelt werden soll, - ein Vorhaben, das mit Fuzzy-Controllern möglicherweise gelöst werden könnte, mit klassischen Regel-Systemen aber fast aussichtslos erscheint.
Im Gegensatz zum Feedbackregler erhält der 'vorwärtsgekoppelte' oder 'Feedforward-Regler' (siehe Abb.2, rechts hinscrollen!) seine Information über den Status des Objekts (Strecke) nicht vom 'Auslauf am Ende' des Objekts (Strecke), sondern von einem Meßort 'vor oder auf' der Strecke, der ganz nahe an der Stelle liegt, an der eine mögliche Störung auftritt. Bei Strecken mit sehr langen 'Durchlaufzeiten' = großen 'Totzeiten' (Beispiel aus chem. Anlagenbau: Extraktionskolonnen, Rektifikationskolonnen, Rohrreaktoren (Drehrohrofen bei Zementfabriken); oder aus der Elektrotechnik: analoge Eimerkettenspeicher, Filterschaltungen mit langen Eigenzeiten) ist ein feedback zum Regler oft so extrem verzögert, daß er versagt. Der Feedforwardregler dagegen erkennt und quantifiziert eine Störung sehr frühzeitig. Aber woher weiß er, welchen Stellwert er einstellen soll, wenn er keine Rückkopplung des Istwerts 'zu sehen bekommt'? Hierzu muß er einfach - salopp gesagt - 'gescheit' sein oder genügend 'Erfahrung besitzen'. Derartige Fähigkeiten können durch jeweils eine der folgenden Alternativen realisiert werden:
Wegen der zu erledigenden komplexen Rechenoperationen muß davon ausgegangen werden, daß für Feedforwardregler immer der Einsatz von digitalen Mikroprozessorsystemen erforderlich sein wird. Der FF-Regler erfaßt eine Störung und berechnet sofort den für ihre Beseitigung erforderlichen Stellwert und gibt diesen auch sofort aus. Er erhält 'theoretisch' kein feedback, - dieses käme ja auch viel zu spät! Dies wird natürlich auch ein Risiko darstellen, dessen Beseitigung oder Eingrenzung in der Praxis sorgfältig gehandhabt werden muß. Hierbei können beispielsweise prozeßbegleitende Expertensysteme von Nutzen sein, die eine Prozeßhistorie erfassen und verwerten (wie etwa: --> 'Vorsicht, vor 2 Tagen ist bei dieser Konstellation die Reaktortemperatur schlagartig angestiegen'). Ein weiterer Vorteil von FF-Reglern ist die grundsätzliche Möglichkeit einer 'Mehrgrößen-Regelung', da ja die Handhabung mehrparametriger Modelle oder multidimensionaler Datensätze mathematisch grundsätzlich möglich ist. Dasselbe gilt für die KI-Methoden. Ein gutes Beispiel hierfür bieten die Applikationen von Fuzzy Controllern, die hervorragend für Mehrgrößenregelungen geeignet sind (--> mehrdimensionale Fuzzy-Matrices).
Spitzfindige könnten übrigens - vielleicht zu recht - feststellen, daß der FF-Regler im Grunde eine konditionelle Steuerung darstellt, - oder gar, daß jede Steuerung eine FF-Regelung sei! Dies sind 'akademische' Streitfragen, den Praktiker wird das sicher wenig erschüttern, Hauptsache es ist anwendbar. Da die Anwendung mit viel Entwicklungsarbeit verbunden ist, wird in der Praxis verständlicherweise nach dem Leitsatz verfahren: 'Alles was klassisch zu bewerkstelligen ist, wird auch auf diese Weise erledigt'. Hierin liegt aber, so vernünftig es auch erscheint, die Gefahr, bei einer attraktiven Methode den Anschluß zu verpassen, - so wäre es den Europäern und Amerikanern hinsichtlich der Fuzzy Controller gegenüber Japan beinahe ergangen!
Um die Eigenschaften der verschiedenen Typen von Reglern, Strecken, Stellgliedern und Meßgliedern verständlich zu machen, soll an dieser Stelle kurz eine der Möglichkeiten erläutert werden, mit denen eine Charakteristik dieser Regelkreiselemente erhalten werden kann. Es handelt sich dabei um die 'Sprungantwortmethode' (siehe Abb.3, rechts hinscrollen!). Bei der Sprungantwortmethode nennt man das zu betrachtende Objekt 'Übertragungsglied'. Das Übertragungsglied wird als 'black box' mit 'Zulauf' uns 'Ablauf' betrachtet. Beim Sprungantwortverfahren wird auf dem 'Zulauf' eine Sprungfunktion aufgegeben und im 'Ablauf' der zeitliche Verlauf der 'Antwortfunktion' registriert. Übertragungsglieder können dabei alle einzelnen Regelkreiselemente, aber auch Zusammenschaltungen derselben sein, wobei natürlich empfehlenswerterweise Rückkopplungsstrukturen zu vermeiden sind, da die Sache sonst etwas kompliziert werden kann. Für eine Typisierung und Charakterisierung der Elemente sind ja auch nur die Einzelcharakteristiken wirklich sinnvoll. Die Sprungantwortmethode entspricht den Verfahren der Ermittlung der Verweilzeitsummenkurve eines Reaktionsapparats in der chemischen Reaktionstechnik, oder besser gesagt: es ist dasselbe!
Dieser Typus von Übertragungsglied soll an erster Stelle stehen, weil seine Charakteristik eigentlich alles bestimmt, 'was zu geschehen hat'. An die Anforderungen der Strecke muß die Art der Regelung, der Reglertyp und dessen Parametrisierung angepaßt werden.
Siehe hierzu Abb.4,(rechts hinscrollen). Strecken mit Ausgleich sind Strecken, deren Charakteristik es ist, nach langer Zeit auf einen stationären Endwert 'einzulaufen'. Beispiel: Ein Metallblock wird mit einer Heizpatrone bei schwacher Heizleistung erwärmt, - es stellt sich eine stationäre Endtemperatur ein. Strecken ohne Ausgleich weisen einen stetigen Signalanstieg auf. Beispiel: Eine Badewanne, die nur durch einen einstellbaren Wasserzulauf gefüllt werden kann (Der Ablauf sei dabei fest verstopft). Anm.: In diesen speziellen Fall einer Füllstandsstrecke wird die Stetigkeit des Anstiegs allerdings durch den Katastrophenfall des 'Überlaufens' abrupt beendet!
Proportionale Strecken sind Strecken mit Ausgleich. Bei einer
Proportionalen Strecke erreicht das Signal am Ausgang für eine am Eingang
aufgegebene Sprungfunktion nach mehr oder weniger zeitlicher Verzögerung
einen Endwert, der ein K-faches (K = proportionaler
Verstärkungsfaktor) der 'Eingangssprunghöhe' erreicht
(Proportionalität).
Eine Art Sonderfall der proportionalen Strecken
soll gleich an dieser Stelle abgehandelt werden:
Eine Totzeit gibt ein Eingangssignal mit der Verstärkung 1 zeitlich verzögert aus, das heißt das Ausgabesignal sieht genauso aus, wie die Signaleingabe, nur erscheint es zeitlich versetzt . In der chemischen Reaktionstechnik entspricht diese Charakteristik der der Verweilzeitsummenkurve eines Idealen Rohrreaktors. In der Elektronik entspräche die Totzeit einem 'idealen analogen Eimerkettenspeicher'.
=========== Teil 2 ===========
Proportionale Strecken werden PTx-Strecken (mit x = 0 bis?) genannt, wobei die Bezeichnung Tx die Charakteristik der zeitlichen Verzögerung kennzeichnet. Eine PTo-Strecke wäre eine Strecke mit einer reinen (proportionalen) Sprungfunktionscharakteristik, also aus praktischen Gesichtspunkten gesehen ein Idealfall. Die Zahl x gibt die Ordnung des Zeitgesetzes der Verzögerung an.
Eine PT1-Strecke ist also eine Strecke, deren zeitlicher Verzug einer Differentialgleichung 1.Ordnung folgt. Beispiele hierfür sind: In der Elektrotechnik: der Tiefpass 1.Ordnung (vgl. Abb. 5 u. 6., rechts hinscrollen); in der chemischen Reaktionstechnik: der kontinuierliche ideale Durchflußrührkessel (KIK). PT1-Strecken sind 1-parametrige Strecken, charakterisiert durch ihre 'Eigenzeit' oder 'Verweilzeit' 'tau'
Strecken höherer Ordnung als 1 sind Strecken mit mindestens 2 Parametern. Ihr Verlauf hat die Form von S-Kurven (siehe Abb. 7, rechts hinscrollen). Bei Strecken des Typus PT3 bis PTn geht man nun in der Regeltechnik-Praxis so vor, daß man ihre Charakteristik durch eine annäherungsweise Parametrisierung mit 2 Parametern in gleicher Weise vornimmt als bei PT2-Strecken. Es werden dabei graphisch 2 sogenannte 'Ersatzzeiten' ermittelt: die Verzögerungszeit Tu und die Verzugszeit Tv. Die Ermittlung geschieht mit Hilfe einer Wendetangenten-Konstruktion (vgl. hierzu Abb. 7, rechts hinscrollen). Man sieht aus der Abbildung, daß die Verzugszeit Tu , eigentlich grob gesagt, die Zeit ist, die es braucht, bis die eigentliche charakteristische Eigenzeitfunktion der Strecke 'losgeht', sie ist also der Totzeit im weitesten Sinne verwandt. Ja man könnte es sogar wagen, eine PTn-Strecke grob anzunähern durch eine Serienschaltung aus einer Totzeit und einer PT1-Strecke (eine Vorgehensweise, die bei der chemischen Reaktionstechnik in Reaktorschaltungen aus idealen Reaktortypen zur Modellierung komplizierter realer Reaktoren grundsätzliche Anwendung findet). Siehe hierzu Abb.8, (rechts hinscrollen). Der Totzeit entspräche dann die Verzögerungszeit Tu (oder umgekehrt) und der Eigenzeit des PT1-Gliedes die Verzugszeit Tv. Die Parameter Tu und Tv einer Strecke können, wie später gezeigt werden soll, zur Einstellung eines Reglers auf die Bedingungen der Strecke verwendet werden.( Für die wenig kennzeichnenden Namen der beiden Ersatzzeiten habe ich mir noch keine Gedächtnisbrücke schaffen können, nur für Tu = vorderes Element in der Zeitkurve, weil 'u' im Alphabet vor 'v' kommt!) . Strecken mit Ausgleich sind in der Praxis einfacher zu handhaben, als solche ohne Ausgleich, sie sind aber erfreulicherweise auch häufiger anzutreffen.
Bei integral wirkenden Übertragungsgliedern ist die Geschwindigkeit, mit der sich die 'output'-Größe ändert, proportional zur Änderung der 'input'-Größe. Es werden integral wirkende Übertragungsglieder ohne Verzögerung (Io - oder ITo - Glieder) und solche mit Verzögerung unterschieden (I1- bis In- oder IT1- bis ITn - Glieder). Vergleiche hierzu Abb. 9, (rechts hinscrollen). Die charakteristische Eigenzeit einer ITn-Strecke Ti , entsprechend Tv bei Strecken vom PTn - Typ, ist bestimmt durch die Steilheit der Antwortkurve. Bei ITo-Strecken ist Ti die Zeit, die benötigt wird, bis die Antwortkurve die Höhe der Erreger-Sprungfunktion erreicht hat. Bei ITn-Strecken mit ausgeprägten Verzögerungszeiten (quasi Totzeiten!), sind diese graphisch abzuschätzen und von der Gesamtzeit abzuziehen, die die Strecke benötigt bis sie den Wert der Erreger-Sprungfunktion erreicht hat. Man hat dann wieder eine 2-parametrige Charakterisierung (Tu und Ti).
Bei einer reinen differentiellen Strecke müßte nach Aufgabe einer Sprungfunktion eine Nadelfunktion als Antwort erhalten werden. Mir sind derartige Strecken nicht bekannt. Nur bei Strecken mit gemischter Charakteristik können, ähnlich wie z.B. bei den PID-Reglern (als andere mögliche Übertragungsglieder), 'D-Elemente' in der Charakteristik enthalten sein. Bei der Sprungantwortkurve muß dann ein 'nadelförmiger Höcker' zu beobachten sein. Ein derartiges Verhalten ist bei der Charakteristik von Stoßdämpfern (möglicherweise auch bei Druckpuffern u.a.) zu beobachten.
Ähnlich wie in der chemischen Reaktionstechnik spielt die Verschaltung von Grundelementen zu komplexeren Gebilden auch in der Regelungstechnik bei allen Typen von Übertragungsgliedern eine Rolle, dementsprechend ebenfalls bei den Strecken. Es ist ein Gemeinplatz festzustellen, daß mit zunehmender Komplexizität der Strecken auch der Systementwurf schwieriger wird. In der Praxis wird man versuchen zu vereinfachen und mit graphischen Lösungen eine Parametrisierung zu erreichen.
An dieser Stelle sollte am besten zunächst die Kategorisierung in stetige und nichtstetige Regler erläutert werden.
Stetige Regler sind durch eine stetige Veränderlichkeit von Istwertsignal und Stellwertsignal gekennzeichnet, d.h. jedem Istwerzustand wird auch stetig ein Stellwertzustand 'zugordnet'. 'Echte' stetige Regler sind im Bereich der elektronischen Regelvorrichtungen deshalb auch immer Analogreglerschaltungen (d.h. Operationsverstärkerschaltungen). Nichstetige Regler sind durch eine in einer oder mehreren Stufen 'fest eingestellte' Stellwertausgabe charakterisiert, d.h. trotz eines stetigen Istwerts wird kein stetiger Stellwert produziert. Bei einer 'festen' Stellwertausgabe, z.B. durch ein Schaltrelais mit einem Schaltpunkt, haben wir 2 Zustände: 'ein' und 'aus'. Diese Regler nennt man Zweipunktregler. Bei mehreren Schaltstufen spricht man von Mehrpunktreglern. Derartige Regler sind meistens für billige 'Konsumerregelungen' geeignet, z.B. die Bimetallthermostate für einfache Elektrogeräte, wie Heizlüfter, Kaffeemaschinen etc. Besonders bei Strecken mit gutem Dämpfungsverhalten sind nichtstetige Regler aber durchaus zufriedenstellend.
Beim Algorithmus von Proportionalreglern wird zunächst die Differenz zwischen Sollwert W und Istwert X, die Sollwertabweichung Xw gebildet, Xw = X - W, und mit dem Proportionalitätsfaktor Kp multipliziert, 'womit' der Stellwert Y erhalten wird: Y = Kp * Xw. Aus dem Verhältnis von erhaltenem Stellwert Y und Xw erhält man umgekehrt den Verstärkungsfaktor Kp (Kp = Y/Xw). Die Sprungantwort eines P-Reglers ist in Abb.10, (rechts hinscrollen) gezeigt. Es sollte an dieser Stelle ganz deutlich realiaiert werden, daß die Sprungantwort eines Reglers keine Regelung darstellt, sondern eine Methode der Charakterisierung des Reglers. Aus der 'möglichst flankensteilen' Antwort im Stellwert ersieht man, daß ein reiner P-Regler vorliegt.
=========== Teil 3 ===========
Wird statt der Stellgröße, wie beim P-Regler, die Stellgeschwindigkeit von der Regelabweichung Xw beeinflußt, dann entsteht ein integrierender Regler. Abb. 11, (rechts hinscrollen) zeigt die formelmäßigen Zusammenhänge und Abb. 12 den Verlauf einer Sprungantwort. Die Zeitkonstante TI eines integralen Reglers ist die Zeit, die er braucht, um nach Anlegen einer Sprungfunktion in der Antwortfunktion die selbe Signalhöhe zu erreichen. KI = 1/TI stellt das Steilheitsmaß der Integralkurve dar.
Reine D-Regler sind technisch nicht realisierbar. Beim differentiell wirkenden Anteil in einem zusammengesetzten Algorithmus wird in der Sprungantwort ein nadelförmiger Peak erzeugt. Die formelmäßigen Zusammenhänge sind in Abb. 13, (rechts hinscrollen) dargestellt.
P-Regler bieten im Regelkreis den Vorteil, daß sie kurze Einregelzeiten haben, besser gedämpft regeln als andere Elemente und eine kleinere Überschwingweite bewirken. Sie haben aber den großen Nachteil einer bleibenden Regelabweichung ( Bei P-Reglern kommt es im Regelkreis häufig dazu, daß der Regler einen 'scheinbar stationären' Zustand in der Stellwertausgabe erreicht, bei dem aber auf der Strecke noch kein Ist-/Sollwertausgleich erreicht wurde. Das Warum? soll an späterer Stelle erklärt werden!).
I-Regler dagegen haben längere Einregelzeiten, eine schlechtere Dämpfung und größere Überschwingweiten. Sie weisen aber keine bleibende Regelabweichung auf.
Diese 'Statements' lassen die Nützlichkeit eines zusammengesetzten Algorithmus erkennen. Der einfachste zusammengesetzte Regelalgorithmus ist deshalb vertsändlicherweise auch der PI-Algorithmus. Dieser wirkt entsprechend der formelmäßig in Abb. 14, (rechts hinscrollen) aufgeführten Terme und stellt im Regelkreis eine Art Synthese beider Eigenschaftsmerkmale dar. Die Sprungantwort von PI-Reglern sieht wie in Abb. 15 exemplarisch gezeigt aus. Statt der Kenngröße KI wird bei der Beschreibung von PI- und PID-Reglern die Nachstellzeit Tn verwendet. Die Nachstellzeit ist die Zeit, die vergehen muß, damit die Sprungantwort wegen der ausschließlichen Wirkung des I-Anteils den Wert erreichen kann, der aufgrund des P-Anteils sofort erreicht wird. Man kann sagen, daß der PI-Regler im Vergleich zum reinen I-Regler um die Nachstellzeit Tn schneller ist. Mit KI = Kp/Tn ist das Steilheitsmaß der Integralkurve festgelegt. Der Reglertyp des PI-Reglers kann auch in den häufigsten Fällen ein gestelltes Regelproblem 'grundsätzlich bewältigen'. Der im nachfolgenden beschriebene PID-Algorithmus kann den PI-Regler eigentlich nur noch in einigen Fällen 'etwas an Tempo übertreffen' ( verknappt und salopp formuliert! )
PD-Regler können zwar technisch realisiert werden, sie bieten aber nur eine Erhöhung der Schnelligkeit gegenüber dem P-Regler, - das grundsätzliche Problem der bleibenden Regelabweichung läßt sich aber mit dem D-Term nicht beseitigen. Ihre praktische Anwendung ist daher sehr selten.
Der PID-Algorithmus stellt die Summe der zuvor behandelten Einzelalgorithmen dar. Abb. 16, (rechts hinscrollen) zeigt die formelmäßigen Zusammenhänge und Abb. 27 eine typische Sprungantwort (in Agilent VEE erzeugt und von einem digitalen PID-Algorithmus stammend). Man sieht die Flanke des P-Anstiegs, den Peak des D-Teils und den schrägen Anstieg des I-Anteils der blauen Kurve.
Anm.: Es handelt sich hier um ein etwas umfangreicheres Spezialkapitel, das über das Standardwissen in Regelungstechnik hinausgeht und das in diesem Rahmen auch nicht erschöpfend behandelt werden kann. Ich verspreche aber, da mir die Sache viel Spaß macht, möglichst viel Info bereitzustellen.
Einleitung (stammt aus meinem Reaktionstechnik-Kurs
für die TU München):
"Time depending processes normally deal
with the course of analogue values with the elapsed time, - a continuous process
in time. Digital devices, like microprocessors, microcontrollers and digital
circuits, are working stepwise in time and in 'variable values' , that means
they exhibit a stepwise quantization of values. The quantization in time is
determined e.g. for micro processors by the processor cycle time, - generally
for digital systems by the 'cycle time'. As you know from your computer that
the accuracy of the values depends on the bit-width of the value ( 8 Bit, 16
Bit, 32 Bit and higher) you also know that the rate of computation mounts with
the processor cycle frequency. This is the basis of all numerical approaches
for time dependent analogue processes by means of digital technique. It is clear
that a stepwise 'treatment' of the steadily running time can only be accurate
enough, when the cycle time is very short in comparison to the whole time ('eigenzeit')
that the process takes. The Shannon-Theorem tells us as a rule that the cycle
frequency should be at minimum 10 times higher than the 'fastest frequency'
of the process."
'Kommunikation'
Wir
müssen nun zunächst einmal dafür sorgen, daß unser
digitales Reglersystem mit der analogen Außenwelt kommunizieren kann.
Dazu müssen die analogen Istwertsignale einer Regelkreis-Strecke
digitalisiert werden, - dies geschieht mit A/D-Wandlern. Ebenso
müssen als 'Output' wieder stetige analoge Stellwertsignale ausgegeben
werden, dies geschieht mit D/A-Wandlern. Die 'lupenreinen' Wandler
wandeln das Analogsignal in ein Digitalsignal entsprechender Bitbreite
(hauptsächlich 8- und 16-Bit = Byte- und Word-Breite!) um - und
umgekehrt. Es gibt auch Wandler nach dem Puls-/Zählerprinzip oder
pseudo-analoge Ausgaben, wie z.B. durch Pulsweitenmodulation, auf all diese
Einzelheiten (die nicht unbedeutend sind!) soll an dieser Stelle nicht
eingegangen werden. Am Ende der angesprochenen Ein-/Ausgabe-Operationen hat das
Digital-System (der Rechner/Mikroprozessor) die Möglichkeit, Werte
aufzunehmen und abzugeben, wir sind jetzt sozusagen soweit, daß wir im
Regelkreisschema hardwaremäßig die Box Analogregler durch eine Box
Digitalregler ersetzen können. An dieser Stelle aber gleich ein Hinweis:
es ist ein leichtes, dem Digitalregler mehrere Istwertkanäle zukommen zu
lassen und ebenso von ihm mehrere Stellwertkanäle bereitzustellen, das
bedeutet, - wenn es uns gelingt mit 'Intelligenz' Algorithmen bereitzustellen,
die das ausnützen, dann können wir sehr leicht
Mehrgrößenregelungen (und zwar mit Verknüpfungen, nicht nur
rein unabhängig parallel) etablieren, - was uns bei Analogsystemen schon
etwas mehr Schwierigkeiten bereitet. Es sollte an dieser Stelle natürlich
auch schon klar erkannt werden, daß reine Zweipunktregler mit
Digitalsystemen besonders leicht realisiert werden können, da der
Stellwertausgang in diesem Fall ja nur ein 1-Bit-Schaltport (Ein/Aus) sein
muß, - aber auch der Regelalgorithmus ist, salopp gesagt, mit 'if...
then... else' schon 'erledigt'! Es bleibt eigentlich lediglich die
Input-A/D-Wandlung.
Jetzt aber zum
Regel-Algorithmus!
Betrachten wir zunächst den feedback-Algorithmus.
Bitte realisieren Sie: es müsste eigentlich nicht zwingend eine Software
entwickelt werden, die gerade den PID-Algorithmus 'emuliert', - man könnte
sich da doch auch 'irgend eine intelligente, vielleicht pfiffige, Sache'
ausdenken, die gut funktioniert und gleichzeitig dem Mikro 'auch besser
schmeckt'! Hierzu gibt es Ansätze, - ein Literaturstudium rentiert sich da
eventuell! Auf jeden Fall Bekanntheit erreicht hat ja inzwischen der
Fuzzy-Regler! . Daß ich diese Alternativen erwähne, liegt daran,
daß ich schon einmal den PID-Algorithmus auf einem Mikro verwirklicht
habe und den Aufwand kenne und deshalb auch den Entwicklern von digitalen
PID-Reglern nicht böse sein kann, wenn einmal ein kleiner 'Mops' in ihrer
Stellwertausgabe zu finden ist, der möglicherweise durch einen Fehler in
der Literatur verursacht ist, der durch zielstrebige 'Weiterzitierung' nicht
auszumerzen war (für Neugierige: im 'Verschiebe-Algorithmus'). Ich
beabsichtige trotzdem, im folgenden die Verwirklichung des PID-Algorithmus in
Software vorzustellen. Bei den Regler-Herstellern wurde der PID-Algorithmus
inzwischen aber zuverlässig funktionierend auf Digitalreglern realisiert,
- es rentiert sich deshalb auch im Normalfall kaum, so etwas 'nachzubasteln'.
Warum etabliert man denn eigentlich den PID-Algo auf Digitalsystemen, wenn er
diesen so ganz grundsätzlich gesehen 'gar nicht so furchtbar gut liegt'
(warum werden Sie noch später sehen!)? Das hat sicherlich zunächst
einmal Kompatibilitäts-Gründe, man will ja häufig existierende
defekte analoge Regler-Syteme ersetzen. Zum anderen ist zum
Regelkreis-System-Entwurf unter Verwendung des PIDALGO am meisten 'know how'
vorhanden. Desweiteren lassen sich die ganzen Optimierungsprozeduren für
PID-Regler gut als zusätzliche 'Begleitung' in der digitalen
(Mikroprozessor-)Reglerelektronik realisieren, da sie meist leicht von den
Mikros ausgeführt werden können (soft- und z.T. auch
hardwaremäßig). Es lassen sich also relativ leicht sogenannte
'autoadaptive' Regler realisieren, - ebenso Hybride aus Fuzzy und PID (man
muß das alles 'nur auf den Mikro kriegen'). Bevor wir nun auf die
grundlegende Programmierung des PID-Algorithmus eingehen, kurz noch eine
weitere 'Einlassung': Man könnte sich vorstellen, daß man in einem
eleganten visuellen Programmiersystem, wie z.B. Agilent (früher HP) VEE
den PID-Algorithmus programmiert und damit in seiner
'Mini-Prozeß-Steuerung' auf diesem System gleichzeitig einen (oder zwei
oder drei??) PID-Regler 'eingebaut' hat. Hiervor möchte ich warnen, Sie
kommen da sehr schnell in Konflikt mit der Zeit (Shannon Theorem!). Das geht
allenfalls dann, wenn Sie lange Eigenzeiten und wenig
Prozeßsteuerungsaufgaben haben, oder wenn Sie nur mal isoliert den
Einsatz eines solchen Reglers testen wollen (hier ist diese Sache sogar ganz
praktisch!), oder - was das gleiche wäre- wenn Sie für den Regler
einzig und allein einen extra PC aufstellen könnten. In der Regel ist es
empfehlenswert PID-Regler als standalone-Elektronik zu betreiben und ihnen,
z.B. über einen Feldbus, nur Parameter (z.B. Sollwert) vom
Prozeßleitsystem zu übergeben oder ihren Istwert 'gelegentlich'
abzufragen etc.
Betrachten wir nun den für stetige Analoggeräte
formulierten PID-Algorithmus in Abb.16 (hinscrollen!),
dann sehen wir, daß wir 'Differential- und Integralmathematik' in der
Formel haben, die unser Analogregler, der ja als analogelektronische Schaltung
eigentlich ein 'Analogrechner' ist, mit 'rasender' Geschwindigkeit abwickeln
kann, ein Digitalsystem dagegen nicht, - weil es, wie oben erläutert, in
quantisierten Zeitschritten arbeitet. Die Umsetzung des PID-Algorithmus in eine
für digitale Mikroprozessoren geeignete Form stellt grundsätzlich das
gleiche Problem dar, wie die 'Echtzeitsimulation' eines in der Zeitskala
stetigen Prozesses. Das Prozedere entspricht dem Entwurf einer 'Logistischen
Gleichung' für den Prozeß. Hierzu wieder ein Textausschnitt aus
meinem obenerwähnten Reaktionstechnik-Kurs, in dem solche
Echtzeitsimulationen eingesetzt werden:
"The logistic equation method is the reverse method of the transition to the
differential quotient starting from the difference quotient in mathematics,
- that means we go back from the infinitesimal value dt = 0 to the very small
value 'delta t' not equal 0, but small in comparison to the 'eigenzeit' , -
i.e. the difference quotient.
Let us take a very simple
example: the differential equation for a linear movement with constant
velocity:
ds/dt = v (v = velocity m/sec, s = distance
m).
The logistic
equation reads:
delta (s)/ delta (t) = v
delta (s) = v * delta (t)
s - sp= v * delta (t)
s = sp+ v * delta (t)
index p = previous, that is
the value of one time step before. If you take more generalized j +1 = index of
new time step, j = index of time step before and 'dt' (but read delta!) for
the very short cycle time (time slice) it reads:
sj+1= sj+ v * dt"
Für unseren PID-Algorithmus bedeutet das, daß wir einfach dt durch die Abtastzeit delta t, im folgenden abgekürzt durch t0, ersetzen, und aus der mathematischen Integration wird die numerische Summierung und aus der differentiellen Änderung der Ist-Sollwertabweichung dXw wird die numerische Differenz delta Xw.Momentanwerte erhalten hier den Index j und zeitlich vorhergehende Werte j-1, j-2 usw. Die direkte Umsetzung ergibt die erste Zeile von Abb. 24 (hinscrollen!), diese Form wird 'Stell-Algorithmus' genannt, weil hier der momentane Stellwert errechnet wird. Die einfachste Realisation eines digitalen PID-Reglers wäre mit einer Programmierung dieser Form möglich. Dies funktioniert zwar, birgt aber das Problem in sich, daß die numerische Berechnung der Summe für den Integralterm mit zunehmender Zeit eventuell 'konsumptiös' werden kann (Term overflow). Dies kann nicht durch ein Begrenzen der Stellwertausgabe beseitigt werden, sondern es müsste schon der Summenterm 'intelligent' überwacht werden! Durch Umformen kann man aber aus der Form 'Stellwert-Algorithmus' eine Form erhalten, in der die inkrementelle Änderung des Stellwerts berechnet wird, diese nennt man 'Geschwindigkeits-Algorithmus', - und wichtig zu beachten: die Summe entfällt hier!. Stellt man diese Form wieder um, indem man nach Yj auflöst, dann erhält man eine Form, die man 'Verschiebe-Algorithmus' nennen kann. In seiner allgemeinen Kurzform mit den Konstanten q0 bis q2 ist dieser in der letzten Zeile aufgeführt. Der Verschiebe-Algorithmus ist für eine Programmierung auf Mikroprozessoren gut geeignet, weil 'nur' Multiplikation und Addition als arithmetische Operationen vorkommen und weil das ganze Objekt inkrementell arbeitet (Division als Multiplikation mit einem Kehrwert! Anm. zu 'nur': bei mir war in der Entwicklungsumgebung keine Bibliotheksfunktion für eine 32-Bit Multipilikation von 16-Bit Werten vorhanden, deshalb betrachte ich aus meiner Erfahrung das 'nur' ziemlich ironisch, denn haben Sie schon einmal einen Multiplikationsalgorithmus in Maschinensprache programmiert?! - aber die Zeiten haben sich geändert, es stehen inzwischen C++-Programmierumgebungen mit umfangreichen Bibliotheken zur Verfügung) . Etwas Milchmädchenrechnung benötigt die Ermittlung der q-Parameter aus den üblichen Einstellparametern Kp, TN und Tv, - siehe Abb. 25 (rechts hinscrollen!). Hier hat sich der Autor (Buch Hoffmann, Digitale Regelung mit Mikroprozessoren), bei dem ich diese Formeln gefunden habe, auch prompt verrechnet (Fehler auf S.20, Umwandlung von Formel 4.3 zu 4.4). Ich hatte dann das Problem, daß mein auf einem Mikroprozessor der 8051-Familie programmierter PID-Regler immer bei der Stellwertausgabe in einem Zweig in eine Sättigung geriet. Ich habe daraufhin den Algorithmus auf dem damals zur Verfügung stehenden Programm Flowchart simulatorisch getestet und dann nach einiger Suche den Fehler gefunden, behoben und erneut getestet, worauf der Algorithmus funktionierte und nach Portierung auf den Mikro ebenfalls klappte. Ich kann aus meiner heutigen Warte interessierten 'Lernenden' nur empfehlen, den Algorithmus einfach einmal so zum Spaß in einem System, wie z.B. Agilent VEE zu testen. Es is schon ein Erfolgserlebnis, wenn es klappt! Bleibt nur noch jeweils eine Tabelle für die Hin- und Zurückrechnungen von Kp, TN und Tv zu den q-Parametern (Abb. 25). Für die q-Werte werden in der Literatur folgende Bereichs-Bedingungen angegeben:
q0 > 0
| q1 | > q0
q1 < 0 = negativ!
| q0+q1 |<q2<q0
Aus Neugier habe ich den Verschiebe-Algorithmus schnell in Agilent VEE 5.0 programmiert und ausprobiert, - und siehe da, es hat funktioniert! Abb. 26 zeigt einen Ausschnitt aus der Entwicklungsumgebung, der die wichtigsten Formelelemente enthält: die Brechnung der q0- bis q2-Werte und den eigentlichen Algorithmus. Abb. 27 zeigt die Regler-Sprungantwort für den programmierten Regler (rot = Istwert-Sprung, blau = Stellwert-Antwort). Nutzer von Agilent VEE oder Leser meines Reaktionstechnik-Kurses, die sich die runtime Version von Agilent VEE 5.0 installiert haben, können das file pidalgo2.vee downloaden und ausprobieren. Dies ist sozusagen auch meine erste Aktion bezüglich der Einrichtung eines Internet Regeltechnik-Praktikums. Der Vorteil dieser Vorgehensweise ist, daß mit Agilent VEE eine universell verwendbare Software benutzt wird.
Nochmals kurz zu der Frage: warum das ganze erarbeiten, wenn empfohlen wird, in der Praxis 'die Finger davon zu lassen'? Na ja, es könnte ja mal passieren, daß Sie doch selbst einen Regler entwickeln 'müssen wollen', der z.B. als hybriden Bestandteil einen PID-Algorithmus enthält. Außerdem: 'Verstehen gibt auch Sicherheit im Anwenden'. Und zuguter letzt: seit meinen Versuchen hat sich viel in der Mikroprozessor-Entwicklungs-Umgebung getan, es ist inzwischen viel bequemer geworden, derartige Syteme zu handhaben (leider sind inzwischen auch die Leute desinteressierter geworden).
Der Fuzzy-Regler
Eine beachtliche Bedeutung unter den Digitalreglern hat nun unumstritten der
Fuzzy-Regler erlangt. Für die Leser, die noch Schwierigkeiten mit der Wirkungsweise
von Fuzzy-Logik haben, sei zunächst mein online-Kurs 'Einführung
in Fuzzy-Logik' 'wärmstens' empfohlen, - dort wird eben gerade ein
'Auto-Abstandsregler' als 'Verständnisbeispiel' vorgestellt (also ein 'feedback-fuzzy').
An dieser Stelle soll noch kurz auf einige unterschiedliche Applikationsmöglichkeiten
von Fuzzy-Logik in Regler-Systemen eingegangen werden, - die Vielseitigkeit
kommt übrigens daher, daß Fuzzy-Logik eben nicht einfach nur ein
'starrer' Algorithmus ist, sondern ein wissensbasiertes KI-System zur 'modellfreien'
Modellierung von Prozessen..Die erste Applikationsmöglichkeit ist,
den Fuzzy-Algorithmus als feedback-Regler-Kern, sozusagen als Ersatz für
den PIDALGO, einzusetzen. Dies entspricht dem 'Abstandsregler' im online-Kurs
zu Fuzzy-Logik. Wichtig ist, in Erinnerung zu behalten, daß dies auch
im 'Mehrgrößenverfahren' möglich ist. Außerdem sind derartige
Regler den klassischen Reglern an 'Stetigkeitssprüngen' im Regelkreisverhalten
meist überlegen.
<< Bild betrachten (VEE Screenshot, ca. 9 kB) >>
Eine weitere interessante Möglichkeit ist, als Regler-Kern den klassischen Regler (PID) zu nehmen und parallel dazu einen Fuzzy-Algorithmus zu schalten, der den klassischen Regler zusammen mit der Strecke sozusagen 'überwacht', dies ist ein adaptives, genauer gesagt ein autoadaptives System. Zusammen mit der Möglichkeit, einmalig oder zu beliebigen Zeiten 'Expertenwissen einfließen zu lassen' ist hier schon sehr viel mehr Flexibilität und Leistung gegenüber dem einfachen PID-Algorithmus gegeben.
<< Bild betrachten (VEE Screenshot, ca. 14 kB) >>
Schließlich noch eine Art Parallelschaltung von Fuzzy- und klassischem Regler:
<< Bild betrachten (VEE Screenshot, ca. 13 kB) >>
hier kann z.B. der Fuzzy-Regler bei Erkennung von starken Unstetigkeiten das 'Regiment' übernehmen, während den 'Routinebetrieb' der klassische Regler übernimmt.
Mit diesen Beispielen und den Kommentaren dazu sind noch lange nicht alle denkabren 'Verknüpfungen' und Operationen des dadurch jeweils erhaltenen Systems vorgestellt, - es soll damit nur gezeigt werden, welche Möglichkeiten grundsätzlich offenstehen. Da die 'Regelungstechnik' in der Praxis ein sehr konservatives 'Metier' zu sein scheint (und das durchaus nicht nur negativ interpretiert), ist es schon ein Erfolg, einmal zum Nachdenken angestossen zu haben!
Schließlich soll noch der Einsatz von Fuzzy-Logik in einem feed-forward-Regler skizziert werden. Der Regler erhält kein feedback vom 'Prozeß-out', sondern nur Störmeldungen von ausgewählten Stellen 'vor oder auf' der Strecke. Diese müssen die Störung nicht nur erfassen und melden, sondern auch quantifizieren. Mit der quantifizierten Störmeldung kann dann die Fuzzy-Logik 'modellfrei' (auf dem 'Expertenwissen basierend') einen Stellwert 'ausdenken', das geht natürlich nur so gut, wie 'Mensch' es 'zusammmengebraut' hat, - da ist schon etwas Vorsicht geboten! Aber elegant ist es schon!
<< Bild betrachten (VEE Screenshot, ca. 13 kB) >>
Bei vielen Einführungen in die Regeltechnik werden die Stellglieder 'heimlich, still und leise' zu den Strecken 'hinzugefügt'. Es wird einfach subsumiert, daß ein ausgegebener Stellwert auf der Strecke den erwünschten Effekt 'erbringt'. Daß dies nicht ganz so einfach ist, sollen zwei Beispiele zeigen. Wie können wir den Füllstand in einer 'Badewanne' regeln, wenn wir nur den Zulaufhahn auf oder zu drehen können? Schon nach der ersten 'Überfüllung' ist 'die Sache gelaufen'! Wir können diese Strecke erst sinnvoll regeln, wenn wir zum Zulauf auch noch die Rückstellkraft Ablauf hinzufügen. Dies bedeutet, daß Stellglieder immer bidirektional wirken können sollten, in Richtung - und vor allem gegen die Richtung - einer Störung. Bei der Beheizung vieler Apparaturen wird mit elektrischen Heizpatronen ein Metallblock mit größerer Wärmekapazität beheizt. Bei der Regelung kann vom Regler nur die Heizleistung zwischen 'aus und voll' verändert werden. Eine Rückstellkraft durch Wärmeabfuhr ist nur durch die Wärmeabstrahlung des Blocks gegeben. Dies stellt eine sehr schlecht regelbare Strecke dar. Die Betreiber versuchen dann, ihr System in einer Art 'Kriechfall-Regelung' hinzutrimmen und sind oft stolz auf die scheinbar erreichte Konstanz! Wehe, es tritt hier eine ernsthafte größere Störung auf, dann zeigt sich der Trugschluß in vollem Ausmaß!
Ein Stellglied ist immer derart einzurichten, daß der im Regler erzeugte Stellwert - der dort ja elektronisch/elektrisch entgegengesetzt zur 'Richtung' der anliegenden Störung ausgegeben wird - auch auf der Strecke einen rückstellenden Effekt erzeugt. Dies muß gegebenenfalls durch elektrische Umformung der Stellwertpolarität etabliert werden. Derartiges kann zum Beispiel bei elektropneumatischen Nadelstellventilen notwendig werden, wenn der Richtungssinn von 'Öffnen'/'Schließen' und elektrischem Stellsignal 'verkehrt' sind.
Merke: Häufig ist es einfacher, an einer Strecke technische Veränderungen vorzunehmen, als sich später mit 'vertrackten Regelproblemen' herumzuschlagen!
=========== Teil 4 ===========
Bei meiner Tätigkeit in der Unterrichtung von Studenten auf dem vorliegenden Gebiet mußte ich feststellen, daß am allerhäufigsten nicht realisiert wird, daß ein ganz grundsätzlicher Unterschied besteht zwischen einer Sprungantwort-Anordnung und einem Regelkreis. Eine Sprungantwort-Anordnung ist sozusagen ein 'offenes' System, sie dient nur zur Charakterisierung von Übertragungsgliedern und kann uns 'nicht direkt aufzeigen, wie sich ein solches Objekt im Regelkreis verhält'. Denn nach erfolgtem Sprung wird dem Objekt ja eine konstantbleibende 'Inputinformation' übergeben ('vorgegaukelt'). Ein Regelkreis dagegen ist ein dynamisch rückgekoppeltes System, bei dem dauernd der 'Inputzustand' abgefragt und bewertet wird und sodann versucht wird eine Änderung vorzunehmen, deren Auswirkung dann wieder den 'Inputzustand' ergibt usw. [ Für ganz 'Gefestigte': Wie stehts' mit einer 'Sprunganwort', bei der auf den Störwert- oder Führungspegel eines 'laufenden' Regelkreises ein Sprung aufgegeben wird? --> Regelungs-Test. Meine Antwort: das Übertragungsglied kann bei Sprungantworten im Sonderfall (oder fast besser gesagt : theoretisch!) auch ein dynamisch rückgekoppeltes System sein (dies wäre dann aber eine ziemlich komplexe 'Strecke' und nicht einfach den elementaren Streckentypen zuordenbar - und gleich gar nicht einfach parametrisierbar!), die Sprungantwort als Vorgang ist aber trotzdem nicht dynamisch rückgekoppelt. Dynamisch rückgekoppelt ist nur das Objekt Regelkreis. (Praktische Bedeutung dürfte eine derartige 'Haarspalterei' aber kaum haben, - habe ich gedacht, - bis mir eine Prüfungsfrage für eine Technikerausbildung untergekommen ist, die mich eines besseren belehrt hat.)]
Für den Praktiker ist es von größtem Interesse, welchen Regler er für seine Strecke wählen soll und wie er ihn einstellen muß, daß das ganze funktioniert.
Bei dieser Methode wird die Sprungantwort der Strecke herangezogen, um den Regler einzustellen. Die Daten sind schon vor Zusammenbau des Regelkreises verfügbar. Zur Einstellung der Parameter Kp, Tn und Tv von P-,PI-,PID-Reglern werden - wie bei der Besprechung der Strecken schon gezeigt - die Ersatzzeitparameter Tu und Tg ermittelt.
Diese Methode arbeitet mit dem fertig aufgebauten Regelkreis. Sie untersucht das dynamische Schwingverhalten des Regelkreises und ist deshalb etwas aussagekräftiger als die Sprungantwortmethode, - allerdings auch weniger einfach durchzuführen. Es wird folgendes Prozedere durchgeführt: der Regler wird im Regelkreis als reiner P-Regler eingestellt. Bei niedrigen Kp-Werten ist ('bei leichtem Anschubsen' durch einen kurzen Störpuls) nach einer kurzen Störung ein gedämptes Einschwingen des Istwersignals im Regelkreis zu beobachten. Bei hohen Kp-Werten wird sich der Regelkreis 'aufschaukeln'. Man sucht sukzessiv durch Probieren den Kp-Wert, bei dem der Regelkreis mit gleichbleibender Amplitude schwingt, - den kritischen Ziegler-Nichols-Punkt. Die Periodendauer dieser Schwingung 'tau-kritisch' und die Verstärkung Kp-kritisch sind die beiden Parameter, die bei der vorliegenden Methode zur Auswertung herangezogen werden.
In der nachfolgenden Zusammenstellung sind die Einstellvorschriften für PI - und PID-Regler nach den beiden Methoden aufgeführt
<< Bild betrachten (Einstellregeln, ca. 7 kB) >>
Zur Erinnerung: Kp = 1 / Xp!
Beispiel für die Regleranpassung an eine Streckenserienschaltung aus Totzeit, PT1- und I-Strecke.
Das vorliegende Beispiel wurde mit Hilfe der Flowlearn-Professional-Software von ehemals Comtec in Aachen ausgeführt, - eine analoge Vorgehensweise auf anderen Systemen, wie z.B. Agilent VEE, ist leicht realisierbar, dabei könnten auch reale Regler verwendet werden, wie z.B. ISM-Moduln mit Anbindung über die serielle Schnittstelle an Agilent VEE. Durch das serielle I-Strecken(-teil-)glied wird die Gesamtstrecke zur Strecke ohne Ausgleich. Es soll gezeigt werden, daß die Anpassung auf eine derartige Strecke genauso funktioniert, wie das Prozedere bei Strecken mit Ausgleich.
Abb.17 (Abb.-Teil 2) zeigt das Blockschaltbild des Regelkreises. Die Aufschaltung einer Störung geschieht in einem Addierer, der einen voreingestellten Störwert nach Zuschalten mit einer 'Relaisschaltstufe' zum Stellwert hinzufügt. Wenn man in dieser Anordnung den PID-Regler durch Setzen von Kp = 0 , Tn = 10000 und Tv = 0 'ausschaltet', kann man eine Streckensprungantwort aufnehmen. Dies ist in Abb.18 (Abb.-Teil 2) gezeigt. Die Streckenelemente sind folgendermaßen parametrisiert: PTT-Glied: Totzeit = 4 sec ; PT1-Glied: Kp = 1 und tau = 2sec ; I-Glied: Tn = 20 sec. Die Sprungantwortkurve ergibt nach der Tangentenmethode für Tu = 5,3 sec und für Tg = 20,3 sec. Man sieht, daß die Wirkung des PT1-Glieds in einem 'Abrunden' des Übergangs von der reinen Totzeit in das reine I-Verhalten besteht. Ein Vergleich von Tu und Tg mit den Parametern der Streckenelemente zeigt, daß die Werte 'vernünftig' sind.
Abb. 19 (Abb.-Teil 2) zeigt den Regelkreis am 'Ziegler-Nichols-Punkt'. Nach der Ziegler-Nichols-Methode wurden erhalten: Kp(kritisch) = 6,11 ; tau(kritisch) = 23,6 sec
Die erhaltenen Einstellwerte sind:
| Sprungantwortmethode | |||
| PI-Regler | PID-Regler | ||
| Kp | 3,8 | Kp | 4,75 |
| Tn | 12,2 | Tn | 10,6 |
| - | - | Tv | 2,2 |
| - | |||
| Ziegler-Nichols-Methode | |||
| PI-Regler | PID-Regler | ||
| Kp | 2,78 | Kp | 3,59 |
| Tn | 20,09 | Tn | 11,82 |
| - | - | Tv | 2,84 |
Abb. 20-23 (Abb.-Teil 2) zeigt die Protokolle der Reglertests mit den erhaltenen Einstellwerten. Abb. 20 zeigt das Protokoll für die Einstellung eines PI-Reglers nach der Sprungantwortmethode. Der Reglkreis schwingt hier noch ziemlich stark, der Regler schafft die Beseitigung der Störung erst nach sehr langer Zeit. Wenn man versucht, nachzuoptimieren, so kann dies sowohl mit einer Rücknahme des Kp-Wertes bei bleibendem Tn-Wert als auch mit einer Erhöhung des Tn-Wertes bei bleibendem Kp-Wert erreicht werden. Ganz allgemein kann beobachtet werden, daß die Einstellwerte für den PI-Regler nach der Sprungantwortmethode noch nachoptimiert werden müssen. Anders ist es dagegen beim PID-Regler nach der Sprungantwortmethode, vergleiche hierzu Abb. 21. Hier beseitigt der Regler die Störung nach 61-62 sec. Dies ist schon bedeutend besser als die Einregelzeit von etwa 102 sec für den PI-Regler nach der Ziegler-Nichols-Methode, deren Verlauf in Abb. 22 gezeigt ist. Auch der PID-Regler nach der Ziegler-Nichols-Methode ist mit ca. 65 sec Einstellzeit, vgl. hierzu Abb.23, nicht besser. Zusammenfassend kann also festgehalten werden, daß mit beiden Methoden gute Einstellwerte für PID-Regler erhalten werden und daß bei der Sprungantwortmethode der PI-Regler nachoptimiert werden muß.
Samal, Grundriß der praktischen Regelungstechnik, Oldenbourg, München, 1974.
Röver, Einführung in die selbständige Regelung, Giradet, Essen.
Oppelt, Kleines Handbuch technischer Regelvorgänge, Verlag Chemie, Weinheim, 1972.
Merz Ludwig, Grundkurs der Regelungstechnik, Oldenbourg, München.
Schlitt Herbert, Regelungstechnik in Verfahrenstechnik und Chemie, Vogel Verlag, Kamprath-Reihe 78, ISBN 3-8023-0124-2.
Krist Thomas, Meß- Steuerungs- Regelungstechnik, Hoppenstedt Verlag, 1987.
Paetzold/Habermann, Meß- und Regelungstechnik, Christiani Schriftenreihe, Konstanz, 1988.
DIN 19226, Regelungstechnik und Steuerungstechnik, Begriffe und Benennungen.
Gute Bücher finden sich im Bereich der E-Technik-Studienliteratur, vor allem auch für Fachhochschulen.
Zur Erstellung von PID-Algorithmen auf Digitalsystemen (Mikroprozessoren):
Hofmann, Digitale Regelung mit Mikroprozessoren, 1983, Vieweg Verlag
Birk, Swik, Mikroprozessoren und Mikrorechner, 1983, 2.Aufl., Oldenbourg Verlag, S. 190- 252
Tip zum Learning by doing:
Kurs Regelungstechnik in ELRAD 1992, Heft 1-12.
Hierbei wird die Software 'Flowlearn/Flowlearn Professional' von ehemals
Comtec in Aachen verwendet, deren Erwerb sehr empfehlenswert wäre,
- die wahrscheinlich aber nicht mehr oder schwierig erhältlich ist. Grundsätzlich
können die Übungen auch auf anderen Systemen, wie z.B. Agilent VEE (früher HP-VEE) (Meilhaus Electronic)
ausgeführt werden.
Meine speziellen Links zu MSR und Datenverarbeitung: Meilhaus Electronic
Weiterer Online-Kurs des Autoren:
Was ist 'Chemische Reaktionstechnik'?
Kleine Wärmelehre (Kalorik)
<< Bild betrachten (Pulsweitenmodulierte Signalausgabe (PWM), ca. 223 kB) >>
Wird, wenn es die Zeit erlaubt, fortgesetzt! Geplant ist u.a. ein Regeltechnik-Praktikum mit auf Agilent VEE simulierten Reglern und Strecken, teilweise mit 'reaktionstechnischen Strecken' aus der Techn.Chemie.
=========== Teil 5 ===========
----------------- -->|
|
|