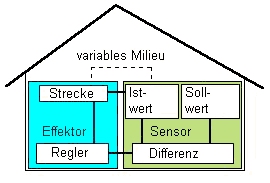
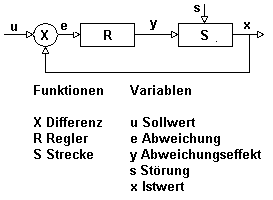
zurück                  Crashkurs  Systemtheorie 2. Ordnung          Inhalt   -   Register   -   Forum       H rückwärts - Seite 86 - vorwärts  


Modellierung

Das nebenstehende Schema zeigt die Abbildung eines Modells, das in bezug auf die Notation ziemlich vage gehalten ist (Anmerkung 1), weil ich bisher damit nur qualitative Aspekte der Erklärung veranschaulicht habe. Wenn ich mit dem Modell simulieren will, muss ich dem Regelkreis Operationen zuschreiben. Regelkreise kann ich formal in verschiedenen Notationen darstellen kann, die äquivalent sind. Ich verwende hier eine beliebige Notation mit drei formalisierten Funktionseinheiten, die in der Regelungstechnik verbreitet ist, da es mir hier nur um das Prinzip geht. Ein System besteht in diesem analytisch-formalen Sinne aus einem Differenz(mechanismus), einem Regler(mechanismus) und einer Strecke, die in Automaten konstruktiv sehr verschieden realisiert sein können:
 

  • Als Differenzbildner bezeichne ich den Mechanismus, mit welchem ich die Abweichung e des Ist-Wert x vom Sollwert u feststelle
  • Als Regler bezeichne ich einen Mechanismus, in welchem aus dem Differenzsignal e eine "Massnahme" abgeleitet y wird
  • Als Strecke bezeichne ich einen Mechanismus, in welchem die Massnahme y umgesetzt wird, wodurch sich der Ist-Wert x verändert, der im nächsten Zeitpunkt wieder mit dem Sollwert u verrechnet wird

    • Bei einer thermostatengeregelten Heizung etwa wird die Differenz zwischen Ist- und Soll-Temperatur in einem Regler interpretiert. Je nach Differenz oder Differenzverlauf wird eine Kompensationsmassnahme im Oelbrenner ausgelöst, was die Temperatur der Heizkörper und mithin die Temperatur des Thermometers (Ist-Wert) verändert, wozu eine "Strecke" vom Brenner der Heizung zum Heizkörper zurückgelegt werden muss, die mit Verzögerungen und Verlusten verbunden ist, und die vor allem auch Perturbationen (Regelungs-Störungen) ausgesetzt ist (Anmerkung 2).


    Die drei Funktionseinheiten im Regelkreis repräsentieren mathematischen Funktionen, die in konkreten Automaten nicht oder nur bedingt konkreten Baugruppen entsprechen (Anmerkung 3).

    Differenzbildner X
    Regler R
    Strecke S

    Ist-Soll-Vergleich
    Kompensationsmassnahme
    Ist-Wertanpassung

    Thermostat
    Signal an Brenner
    Zustand der Heizkörper

    u - x = e
    y(N) = Kp*e(N) + Ki*Summe (E(N) + Kd*delta e(N) [für PID-Regler]
    x(N) + T1*dx(N) + T2 * dx hoch2 (N) = Ko * y(N)

    Regler und Strecke werden in der System Dynamics durch zeitabhängige Formeln programmiert. Die "Ks" im Regler stehen für Parameter, die Indexe der "K"s, also p, i und d für die mathematischen Funktionen in den Teilformeln: proportional, integral und differential. Die "Ts" und "Ko" in der Strecke sind ebenfalls Parameter. Das "delta x" und das "delta hoch 2" führen durch die Ersetzungen delta x(N) = [x(N) - x(N-1)] ein "Gedächtnis" ein, das Werte der vorangehenden Taktzeitpunkte berücksichtigt. Regler und Strecken können also in Abhängigkeit der Anzahl der Formelteile unterschiedliche Kompliziertheit aufweisen. Primitive Strecken berücksichtigen nur die momentane Differenz zwischen Ist- und Soll-Wert, kompliziertere Strecken berücksichtigen Widerstände und Trägheit, wozu sie eine Art Gedächtnis brauchen (Anmerkung 4).

    Ganz einfache Modelle setzen alle Parameter auf Null, so dass sie in den Formeln weggelassen werden können.


    Anweisungen:

    Konstruiere ein ganz einfaches quantitatives Modell einer Heizung und schaue, wie sich das Modell verhält!

    		     

    Was mit dem Computer geht, kan man ja - im Prinzip - auch auf einem Blatt Papier durchspielen. Man ist dann quasi ein Modell des Computers - wie das Modell des Künsters quasi invers ein Modell seines Bildes ist.

    Man kann beispielsweise so verfahren:
    Nachdem man die Operationen definiert hat, kann man mit einem Anfangszustand zum Zeitpunkt t=0 beginnen und für die weiteren Zeitpunkte t=1, t=2, usw berechen, wie sich der Zustand des Systems verändert. Dabei schreibt man eine Tabelle, in welcher die Variablen als Funktion ihrer Werte fortgerechnet werden.

    Eine Heizung braucht natürlich einen Sollwert und einen abweichenden Ist-Wert, damit überhaupt etwas passiert.

     

    Beispiel:
      klick hier

    		    

     

    Metakommunikation

    Die System Dynamics kann man als praktische Anleitung dazu verstehen, mit welchem Formalismus, man welche Zahlenreihen produzieren kann. Die Simulation ist dann quasi die Verfikation des gewählten Formalismus.

    Auf den Spielaspekt gehe ich unter Spielsimulation näher ein.


     
     top                  Crashkurs  Systemtheorie 2. Ordnung          Inhalt   -   Register   -   Forum       H rückwärts - Seite 86 - vorwärts  

    Crashkurs Systemtheorie