Orthogon ist ein Fremdwort für Rechteck.
|
Orthogon ist ein Fremdwort für Rechteck. |
|
Als ortogonal bezeichne ich .... die Position senkrecht ... das Lot hat auf beiden Seiten denselben Winkel ... Wenn ich eine Mauer herstelle, verwende ich ein Lot. Wenn der Grund der Mauer horizontal verläuft, habe ich auf beiden Seiten der Mauer denselben Winkel - Warum sollt mich der Winkel interessieren ? In der Elementargeometrie nennt man zwei Geraden oder Ebenen orthogonal (bzw. senkrecht), wenn sie einen rechten Winkel, also einen Winkel von 90°, einschließen. Die beiden Strecken [ A B ] {\displaystyle [AB]} {\displaystyle [AB]} und [ C D ] {\displaystyle [CD]} {\displaystyle [CD]} sind orthogonal, da sie miteinander einen rechten Winkel bilden. Zwei Vektoren heißen orthogonal, wenn sie auf zueinander orthogonalen Geraden liegen oder wenn mindestens einer der beiden Vektoren der Nullvektor ist. Dies ist gleichbedeutend damit, dass ihr Skalarprodukt null ist. Diese Eigenschaft wird in der linearen Algebra zur Definition von Orthogonalität in allgemeinen euklidischen Vektorräumen erhoben: Zwei Vektoren heißen zueinander orthogonal, wenn ihr Skalarprodukt null ist. Diese Bedeutung wird auch auf Abbildungen zwischen Vektorräumen übertragen, die das Skalarprodukt und damit die Orthogonalität zweier Vektoren unverändert lassen. |
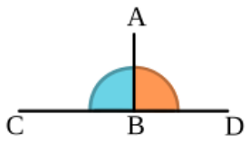
Bildquelle: Wikipedia |