"2. Ordnung" hat sehr viele sehr verschiedene Bedeutungen (siehe Anmerkungen unten). Hier behandle ich eine sehr spezifische Verwendung des Ausdruckes, die ich meine, wenn ich von Systemtheorie 2. Ordnung und von Beobachtung 2. Ordnung spreche. Vergleiche dazu auch Beobachten und die 2. Ordnung und Konstruktivismus - Die 2. Ordnung.

Mit "2. Ordnung" bezeichne ich nicht den Rang einer Klassifikation oder einer Entwicklungsstufe, also nicht, was beispielsweise in der Biologie oder in Bezug auf Landstrassen als Ordnung bezeichnet wird, sondern eine Art reflexive Verdoppelung beim Beobachten, die durch eine gewählte Selbstbezüglichkeit entsteht, wenn ich eine Beschreibung beschreibe. In der 2. Ordnung beschreibe ich nicht das Referenobjekt der beschriebenen Beschreibung, sondern wie dieses beschrieben wurde.

Anmerkungen zum Kontext und einigen Komplikationen

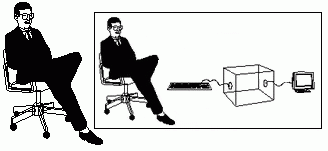
H. von Foerster hat diese 2. Ordnung als Cybernetics of Cybernetics eingeführt, in welcher der Systemtheoretiker als Objekt seiner Theorie, also als System erscheint, das seine Umwelt als Blackbox erkennt. In der konventionellen Wissenschaft generell und auch in der konventionellen Kybernetik wird nur das untersuchte Objekt beschrieben, weil der Beobachter keine Rolle spielt, da ja jeder Beobachter dasselbe, das objektiv Richtige sieht. Deshalb kommt der Beobachter dort gar nicht vor.
Auch in der philosophischen Erkenntnistheorie fehlt der Beobachter.

Das Konzept dieser 2. Ordnung hat H. von Foerster anhand der Vorstellung eingeführt, dass das Präfix „Selbst-“ durch den Begriff ersetzt werden kann, dem es vorangestellt ist Aus Selbstbeschreibung wird so die Beschreibung einer Beschreibung (Observing Systems, S.177 [ ]) Der Beobachter wurde von H. Maturana durch die Aussage, dass jede Aussage von einem Beobachter stammt, eingeführt. Zusammen mit H. von Foerster postulierte er, dass der Beobachter beobachtet werden muss, was zu einem wesentlichen Merkmal des Radikalen Konstruktivismus geworden ist. Die Kernidee lautet: Kybernetik erster Ordnung: der Kybernetiker beobachtet Systeme. Kybernetik zweiter Ordnung: der Kybernetiker beobachtet sich selbst als System, das seine Umwelt beobachtet. Der Beobachter wird damit zu einem Teil oder zu einem Aspekt des beobachteten Systems. Der Beobachter und was er beobachtet, blieb aber bei H. Maturana weitgehend unbestimmt - und nur in Beispielen wie etwa dem U-Boot-Kapitän, der seine Umwelt nicht sehen kann, erläutert, was viele (Miss)Verständnisse verursachte. Weil Menschen in in seiner Theorie keine Rolle spielen, hat N. Luhmann vorgeschlagen, nur noch von Beobachtungen und nicht mehr vom Beobachter zu sprechen. In seiner Beobachtung 2. Ordnung ist der Beobachter aufgehoben. Ich unterscheide zwei Fälle, wovon ich nur den zweiten als Beobachtung 2. Ordnung bezeichne: Im einen Fall beobachtet ein Beobachter andere Beobachter - aber nicht sich selbst -. Diese Variante hat sich in der Soziologie verbreitet, wo oft von einer 2. Ordnung gesprochen wird, wenn ein Beobachter einen anderen Beobachter beobachtet, etwa wenn ein Soziologe einen Journalisten beobachtet, der etwas - beispielsweise tote Fische im Rhein - beobachtet. In diesem Fall wird der Ausdruck Beobachter in einem umgangssprachlich konventionellen Sinn vrwendet. Im anderen Fall - den ich mit der 2. Ordnung bezeichne - beobachte ich die Umwelt des Beobachters als Blackbox. Es handelt sich um eine Inversion, durch welche die Umwelt aufgehoben wird. Ich kann dabei nicht erkennen, ob oder inwiefern die Umwelt richtig dargestellt wird, sondern nur was wie als Umwelt beobachtet wird. Dabei beobachte ich die Beobachtungen, nicht den Beobachter. Es geht es dabei um Beobachtungen von Unterscheidungen, die der beobachtete Beobachter macht. N. Luhmann verwendet Beobachtung 2. Ordnung in diesem Sinne. Indem er aber den Beobachter ausblendet, lässt er zu, dass Beobachtungen von Organisationen gemacht werden können, obwohl eine Organisation weder sprechen noch schreiben kann. Erläuterungen anhand eines Beispiels:

In der umgangssprachlichen Verwendung von beobachten ist aufgehoben, ob die Beobachtung dokumentiert oder wenigstens zur Sprache gebracht wird. Hier interessiert aber nur der Fall, in dem das Beobachtete beschrieben wird. Wenn ich sehe, dass jemand mit einem Feldstecher längere Zeit an einen bestimmte Ort schaut, nehme ich an, dass er etwas beobachtet. Aber nur wenn er beschreibt, was er beobachtet, wird es auch für mich eine Beobachtung.

Als Beobachtung bezeichne ich in diesem Sinne ein manifestes Resultat des Beobachtens, beispielsweise einen Bericht darüber, was wie beobachtet wurde. In jeder Beobachtung in diesem Sinn wird ein beobachteter Gegenstand bezeichnet und über ihn etwas gesagt, im einfachsten Fall: „x ist y“, beispielsweise „Das Auto ist rot“.

Wenn ich die Beobachtung – also nicht das Referenzobjekt der Beobachtung – beobachte, spreche ich von einer Beobachtung 2. Ordnung. Ich kann dann etwa sagen, dass in der Aussage von einem Auto die Rede ist oder dass die Aussage von xy gemacht wurde. Dabei sage ich nichts über das Auto und dessen Farbe. Da es sich wieder um eine Beobachtung handelt, muss auch sie explizit sein.

Eine spezielle Art der Beobachtung 2. Ordnung beobachtet Unterscheidungen, die in der beobachteten Beobachtung verwendet wurden. Ich beobachte beispielsweise, dass von einem Auto und rot die Rede ist, und frage mich, was dabei wovon unterschieden wird. Rot ist eine Eigenschaft des Autos, die ich als Wert der Eigenschaftsdomäne Farbe erkenne. Das, was in der Beobachtung unterschieden wird, bezeichne ich als Wert einer Kategorie. In der Beobachtung, dass das Auto rot ist, wurde die Kategorie Farbe gewählt. Die Eigenschaft gehört zum Auto, die Kategorie zur Beobachtung.

Das systematische Beobachtung von Kategorien bezeichne ich als theoretisieren. Als Theorie bezeichne ich eine explizite Reflexion (Widerspiegelung) der Kategorien, die ich beim Beobachten von Sachverhalten verwende. Theorie ist mithin ein Resultat einer Beobachtung 2. Ordnung. Sie beschreibt die Anschauung (theorein), nicht das Angeschaute.

Anmerkungen:
 
Es gibt Landesstraßen zweiter Ordnung, Differentialgleichung zweiter Ordnung, Erbfolger zweiter Ordnung, ...
 
Oft wird 2. Ordnung für 2. Ebene oder für eine höhere Stufe von Ordnung verwendet. H. Maturana etwa spricht von "Systemen 2. Ordnung" und meint damit beispielsweise Metazeller, die Systeme aus Einzellern sind.
 
Ein Fehler 2. Ordnung heisst beispielsweise, wenn jemand aus der Ferne ein ein Stück Nahrung für einen Fressfeind hält und deshalb auf die Nahrung verzichtet (der Schaden ist relativ klein). Ein entsprechender Fehler 1. Ordnung ist - in dieser Redeweise - wenn jemand einen Fressfeind für Nahrung hält und deshalb selbst gefressen wird (der Schaden ist - nicht relativ - gross). (In der Statistik wird in diesem Zusammenhang anstelle von Ordnung oft Art gesprochen).