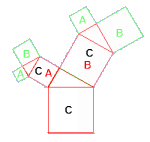
Der Ausdruck "Fraktal" stammt - terminologisch gebunden - von B. Mandelbrot und bezeichnet in der Mathematik eine spezifische Rekursion, die in dem Sinne als "Selbstbeinhaltung" gesehen werden kann, als ein Objekt aus rekursiv verkleinerten Kopien seiner selbst besteht.
Beispiel:
Eine Bibliothek ist in dem Sinne "fraktal", als die einzelnen Abteilungen der Bibliothek und die Bücher in den Abteilungen und die Aufsätze in den Büchern alle wie die Bibliothek selbst organisiert sind. Die Bibliothek hat Räume, die Werk haben Bände, die Bände haben Kapitel, die Kapitel habe Abschnitte. Die Bibliothek hat ein Register, die Bücher haben Inhaltsverzeichnisse.
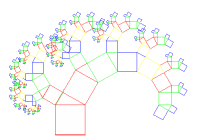
Fraktale beschreibe ich durch rekursive Operationen, die prozedurale Ordnungen aufdecken, die etwa in Form von Umrissen nicht fassbar sind. Einen Baum (nebenstehendes Beispiel) beschreibe ich als ein "Sich-Verzweigen", respektive als Resultat einer rekursiven Operation, die auf einer rekursiv verkleinerten Basis erfolgt.
Beim natürlichen Baum ist die Verzweigung immer gleich gross, aber die frühen Verzweigungen wachsen sich zu Stamm und Ästen aus bis die jeweils jüngsten Verzweigungen an den Astenden erfolgen.
Ich kann deshalb einen Ast rekursiv als relativen Stamm mit Ästen sehen, also eine Wiederholung eines Musters erkennen.
Fraktale bilden einen Aspekt der Chaostheorie